Wie Funktioniert eigentlich ein Venturirohr?
.
„Wenn keiner was wegnimmt und keiner was dazu tut, dann bleibt alles, wie es ist.“ Diese Erfahrung bestätigt sich für die meisten Menschen bereits in den ersten Lebensjahren. Und, einmal verinnerlicht, kann dieses Gesetz immer wieder hervorragende Erklärungen liefern, wie im Fall eines Venturirohres.
.

.
Eine Verjüngung oder, anders gesagt, eine Querschnittsreduzierung weist äußerlich auf dieses Bauteil hin. Es kommt gänzlich ohne Mechanik aus und bewirkt doch beachtliches. Das Venturirohr kann die Zustände in einer Rohrleitung so enorm verändern, dass es von einer Druck zu einer Saugerscheinung kommt. Eben noch hat das Wasser, welches durch ein Rohr gepresst wird, die Wandung dieses Rohres kräftig nach außen gedrückt, und im nächsten Moment soll es diese Wandung nach innen ziehen? Richtig gelesen?! Genau dieses Phänomen lässt sich durch das Venturirohr bewirken.
.
Reduzierung des Problems
Druck ist aus dem Verständnis der Bernoulli-Gleichung zusammengesetzt aus statischem Druck, Schweredruck und dynamischen Druck. Versucht man mittels Daumen eine soeben angebohrte Wasserleitung zu schließen, teilt sich einem der statische Druck am Daumen mit. Taucht man im Schwimmbad auf eine Tiefe von 2,50 Metern, so verspürt man deutlich den Schweredruck des Wassers auf den Ohren. Und hält man die Hand in einen fließenden Bach, spürt man die Bewegung des Wassers als einen Druck, eben den dynamischen Druck. Wir reduzieren für die weiteren Gedankenmodelle die Theorie auf nur noch den statischen und den dynamischen Druck. Ein 15er Kupferrohr sei daher absolut waagerecht verlegt. Eine zehn Meter hohe Talsperre im Hintergrund sorgt für immer gleichmäßig nachströmendes Wasser mit einem (aus diesen zehn Metern) resultierenden Überdruck von 1 bar. Dieses 15er Rohr wird am Ende mit einer Kappe verschlossen. Auf der Rohrinnenwand lastet nun ein Druck von 1 bar. Selbst wenn man diese Kappe abnimmt und das Wasser ausströmt, verliert die Talsperre nur unwesentlich Wasserhöhe und damit Druck. Würde das Stauwasser höher aufgestaut, würde das geschlossene Rohr einem höheren Druck ausgesetzt. Das geöffnete Rohr würde bei größerer Stauhöhe schneller durchflossen, ebenfalls wegen des höheren Drucks. Aber für das nachfolgende Modell bleibt der Wasserspiegel konstant bei zehn Metern.
.
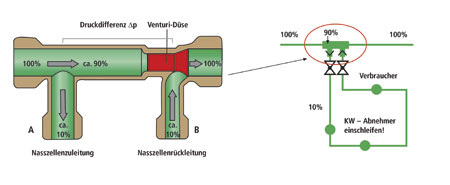
.
Modell im Fluss
Nun wird also die Kappe abgenommen und der Druck von 1 bar würde zumindest teilweise umgewandelt in Bewegungsdruck und einen gewissen restlichen Anteil an statischem Druck. Dieser statische Druck würde weiterhin gegen die Rohrwand drücken. Der dynamische Druck einer Flüssigkeit ergibt sich aus:
.

.
Am Ende des Rohres wird in diesem Gedankenexperiment festgestellt, dass das Wasser mit einer Geschwindigkeit von fünf Metern pro Sekunde austritt. Daraus folgt, dass der dynamische Druck im Rohr errechenbar ist und sich wie folgt ergibt:
.
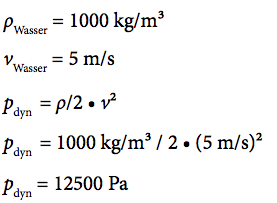
.
Wenn also ursprünglich 1 bar, also 100 000 Pa zur Verfügung standen, so verbleiben jetzt noch 100 000 Pa minus 12 500 Pa, also 87500Pa (oder eben 0,875bar) als Belastung für die Rohrwand. Und nun kommt bei diesem noch recht übersichtlichen Gedankenexperiment die erste Änderung ins Spiel: Jemand drückt – oder besser hämmert – auf dem Kupferrohr herum. Der Querschnitt an dieser Stelle des Rohrs wird reduziert. Es tritt aber weiterhin der gleiche Volumenstrom am Ende des Rohres aus. Folglich muss das Wasser an dieser Delle im Rohr schneller fließen als im unversehrten Rohr. Die Delle im Rohr sei in diesem Experiment so erheblich, dass nur noch die Hälfte der Querschnittsfläche des Rohres übrig bleibt. Die Folge ist selbstverständlich: Das Wasser muss hier doppelt so schnell vorbei, also mit zehn Metern pro Sekunde. Und für den dynamischen Druck gilt dann:
.

.
Die Rohrwand ist durch das schnelle Fließen an dieser Stelle erheblich entlastet worden. Der Druck auf die Rohrwand hat sich gegenüber dem Ruhezustand auf nur noch (100 000 Pa minus 50 000 Pa) 50 000 Pa halbiert. Und bei weiterer Zunahme der Geschwindigkeit, als Folge eines immer kleineren Durchlasses an dieser Delle, ließe sich diese Änderung weiter verstärken.
.

.
Leck, das Luft ansaugt
Gedanklich könnte man die verbleibende Fläche nochmals halbieren und die Geschwindigkeit an dieser Stelle damit nochmals verdoppeln, also auf 20 m/s erhöhen. Nach bereits bekannter Gleichung gilt dann:
pdyn = 1000 kg/m3 / 2 • (20 m/s)2 pdyn = 200 000 Pa
Nur durch diese Querschnittsveränderung und der damit einhergehenden Beschleunigung des Wassers ist der dynamische Druck auf 200 000 Pascal oder eben 2 bar angestiegen. Spätestens jetzt merkt man die Schieflage. Denn 100 000 Pa minus 200 000 Pa ergeben minus 100 000 Pa. Der Stausee liefert ja auch nur 1 bar, also 100 000 Pa. Wie wirkt sich also diese Delle in der Praxis aus? Die Differenz verursacht tatsächlich einen Unterdruck (oder physikalisch korrekt „negativen Überdruck“). Würde man mit einem winzigen Bohrer ein Loch in diese Delle bohren, so würde nicht etwa Wasser herausspritzen, sondern Luft hineingesogen. Würde man anschließend jedoch die Kappe auf das Ende des Rohres setzen und damit die Fließgeschwindigkeit auf Null reduzieren, würde Wasser aus dieser Bohrung austreten. Klar, denn der Druck auf die Wandungen des Rohres würde wieder 1 bar betragen. Zurück zu der Erfahrung aus der Kindheit: „Wenn keiner was wegnimmt und keiner was dazu tut, dann bleibt alles wie es ist.“ Wenn also äußerlich der Druck unverändert bleibt (Stausee mit 10 Meter Stauhöhe), dann ist dieses System insgesamt im Gleichgewicht. Der resultierende Druck muss also konstant bleiben. Bei steigendem dynamischen Druck kann der Druck auf die Rohrwand nur abnehmen.
.

.
Und in der Praxis?
Zuerst einmal ist die Formel von Bernoulli idealisiert angenommen. Man geht nämlich von einer reibungsfreien Flüssigkeit aus. Die Delle aus dem Gedankenexperiment würde in der Realität den Fließwiderstand des Wassers im Rohr erhöhen und insgesamt würde der Volumenstrom gegenüber einer Installation ohne Delle ein wenig abnehmen. Der Rest der Überlegungen stimmt jedoch und wirkt sich auf praktische Anwendungen auch in der Sanitär- und Heizungstechnik aus.
.
Beispiel Perlator (auch Luftsprudler oder Strahlregler genannt):
An Mischbatterien und ebenso in modernen Brauseköpfen nutzt man den Venturieffekt um Luft in den Wasserstrahl zu mischen.
Beispiel Wasserschalter: Gas- oder Elektro-Durchflusswassererwärmern ist das Venturirohr ebenfalls eingebaut. Man provoziert den Unterdruck hier meistens, um einen Schalter zu betätigen.
Beispiel Wasserstrahlpumpe: In der Düse einer Wasserstrahlpumpe sinkt der statische Druck im Betrieb so stark, dass er niedriger als der Luftdruck wird. Der Luftdruck drückt dann seinerseits das Wasser in den Pumpenraum und fördert es fort. So eine Pumpe hat keine beweglichen Teile und daher so gut wie keinen Verschleiß. Sie ist auch weitestgehend unempfindlich gegen Schmutz und Chemikalien. Für eher seltene Pumpaktionen ist die Wasserstrahlpumpe daher oft ausreichend wirksam und durchaus einsetzbar.
Beispiel Gasdüsen an Brennern oder Rezirkulation in Brennern:
Um einen sogenannten atmosphärischen Brenner ohne Gebläse zum Laufen zu kriegen, bedient man sich auch des Venturi-Prinzips. An der Ansaugstelle für die Primärluft wird das Gas so sehr beschleunigt, dass es an dieser Stelle einen ausreichenden Unterdruck zum Transport der Luft erzeugt. Sogenannte Rezirkulationsbrenner (auch Blaubrenner genannt) nutzen das Venturi-Prinzip um bereits verbranntes Abgas nochmals durch die Flamme zu jagen.
.Venturi sorgt für Hygiene
Neuerdings hat die Sanitärindustrie den alten Venturi ebenfalls wiederentdeckt. Man setzt ein Venturirohr ein um Stagnation, beispielweise in zeitweise unbenutzten Hotelzimmern, zu verhindern. Dazu schleift man eine gefährdete Installation am Steigestrang und gewährleistet so eine Durchströmung bei jedem Wasserfluss in der Steigeleitung. Diese Kunstgriffe innerhalb der Technik des Anlagenmechanikers sind allesamt vorteilhaft für die jeweilige Anwendung. Es sind in der Praxis der Heizungstechnik aber auch Nachteile bekannt, die auf den Venturi-Effekt zurückzuführen sind:
.
Beispiel Lufteintrag in Heizungsanlagen: In normalen Kellerzentralen einer Heizungsanlage schwindet zwischen den jährlichen Wartungen regelmäßig ein Teil des Heizungswassers. Der Druck fällt dadurch naturgemäß ein wenig ab. Dies wirkt sich besonders für die Heizkörper des obersten Geschosses aus. An den Heizkörpern sind nämlich üblicherweise auch Thermostatventile montiert. Der Durchlass an diesen Ventilen ist immer mit einer Querschnittsverengung einhergehend und ruft damit auch immer den Venturieffekt hervor. Bei diesem Zusammentreffen von Ereignissen, also geringer Anlagendruck und hohe Geschwindigkeit an diesem Systempunkt kann der Druck in diesem Ventil so gering werden, dass auch Luft von außen in die Heizungsanlage gezogen (eigentlich durch den Luftdruck hereingedrückt, Verzeihung liebe Berufsschullehrer) wird.
Merke: „Wasserdicht heißt nicht zwangsläufig gasdicht“ Mit dem Sauerstoff holt man sich natürlich auch wieder Korrosionspotenzial, sprich Rost, ins Haus. Eine gut gefüllte Heizungsanlage und ein richtig dimensioniertes Ausdehnungsgefäß stellen daher tatsächlich einen Schutz vor Korrosion dar.
So weit lässt sich also der Venturi-Bogen für den Anlagenmechaniker spannen. In der zivilen Welt sind ebenfalls Anwendungen des Venturiprinzips zu finden. Die alten Vergaser vergangener Autotage saugten und mischten Benzin mit Luft nach dieser Methode. Parfumzerstäuber und Farbspritzgeräte arbeiten ebenfalls nach diesem Prinzip.